多维数据可视化是指通过一些手段将高维的数据展示在二维的平面中,在进行探索性数据分析及对聚类或分类问题的验证中有着重要的应用。本文将介绍一些常用的多维数据可视化的方法。
首先请出万能的鸢尾花数据。
import pandas as pd
data = pd.read_csv('https://raw.github.com/pydata/pandas/master/pandas/tests/data/iris.csv')
data.head()
可以看到其中包含5列,前四列是特征,name是分类
SepalLength SepalWidth PetalLength PetalWidth Name
0 5.1 3.5 1.4 0.2 Iris-setosa
1 4.9 3.0 1.4 0.2 Iris-setosa
2 4.7 3.2 1.3 0.2 Iris-setosa
3 4.6 3.1 1.5 0.2 Iris-setosa
4 5.0 3.6 1.4 0.2 Iris-setosa
下面来看一下如何对有四个特征的数据进行可视化。
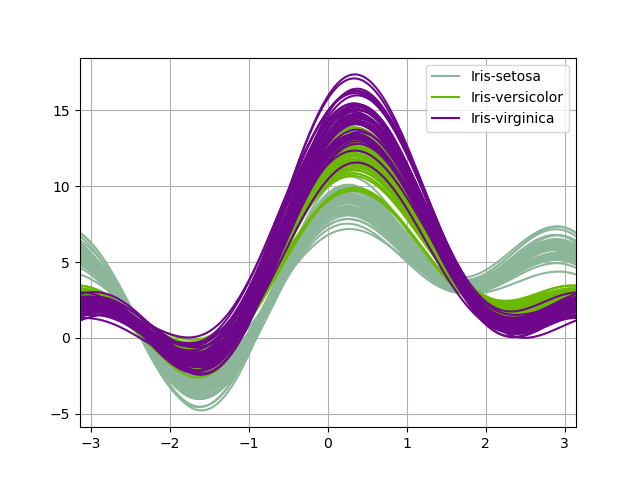
Andrews曲线
Andrews曲线将每个样本的属性值转化为傅里叶序列的系数来创建曲线。通过将每一类曲线标成不同颜色可以可视化聚类数据,属于相同类别的样本的曲线通常更加接近并构成了更大的结构。
from pandas.tools.plotting import andrews_curves
plt.figure()
andrews_curves(data, 'Name')
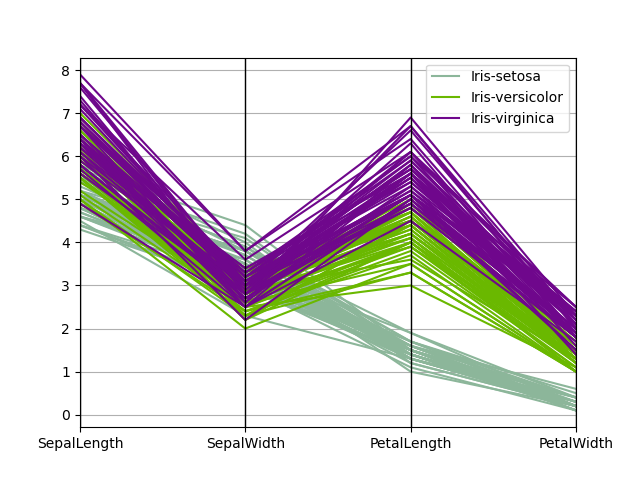
平行坐标
平行坐标也是一种多维可视化技术。它可以看到数据中的类别以及从视觉上估计其他的统计量。使用平行坐标时,每个点用线段联接。每个垂直的线代表一个属性。一组联接的线段表示一个数据点。可能是一类的数据点会更加接近。
from pandas.tools.plotting import parallel_coordinates
plt.figure()
parallel_coordinates(data, 'Name')
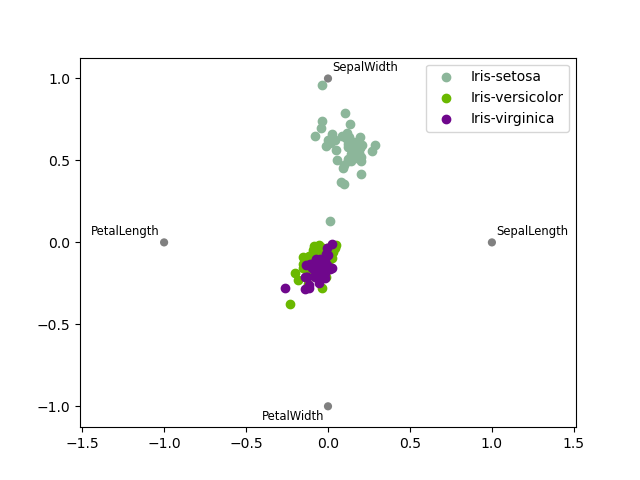
RadViz(雷达图?)
RadViz是一种可视化多维数据的方式。它基于基本的弹簧压力最小化算法(在复杂网络分析中也会经常应用)。简单来说,将一组点放在一个平面上,每一个点代表一个属性,我们案例中有四个点,被放在一个单位圆上,接下来你可以设想每个数据集通过一个弹簧联接到每个点上,弹力和他们属性值成正比(属性值已经标准化),数据集在平面上的位置是弹簧的均衡位置。不同类的样本用不同颜色表示。
from pandas.tools.plotting import radviz
plt.figure()
radviz(data, 'Name')
因素分析(FactorAnalysis, FA)
因素分析最初心理学家斯皮尔曼发明,用于研究人类的人格特质,著名的卡特尔16PF(16种相对独立的人格特征)就是应用因素分析方法得来。基于高斯潜在变量的一个简单线性模型,假设每一个观察值都是由低维的潜在变量加正态噪音构成。
from sklearn import decomposition
pca = decomposition.FactorAnalysis(n_components=2)
X = pca.fit_transform(data.ix[:,:-1].values)
pos=pd.DataFrame()
pos['X'] =X[:, 0]
pos['Y'] =X[:, 1]
pos['Name'] = data['Name']
ax = pos.ix[pos['Name']=='Iris-virginica'].plot(kind='scatter', x='X', y='Y', color='blue', label='Iris-virginica')
ax = pos.ix[pos['Name']=='Iris-setosa'].plot(kind='scatter', x='X', y='Y', color='green', label='Iris-setosa', ax=ax)
pos.ix[pos['Name']=='Iris-versicolor'].plot(kind='scatter', x='X', y='Y', color='red', label='Iris-versicolor', ax=ax)

主成分分析(PCA)
主成分分析是由因子分析进化而来的一种降维的方法,通过正交变换将原始特征转换为线性独立的特征,转换后得到的特征被称为主成分。主成分分析可以将原始维度降维到n个维度,有一个特例情况,就是通过主成分分析将维度降低为2维,这样的话,就可以将多维数据转换为平面中的点,来达到多维数据可视化的目的。
from sklearn import decomposition
pca = decomposition.PCA(n_components=2)
X = pca.fit_transform(data.ix[:,:-1].values)
pos=pd.DataFrame()
pos['X'] =X[:, 0]
pos['Y'] =X[:, 1]
pos['Name'] = data['Name']
ax = pos.ix[pos['Name']=='Iris-virginica'].plot(kind='scatter', x='X', y='Y', color='blue', label='Iris-virginica')
ax = pos.ix[pos['Name']=='Iris-setosa'].plot(kind='scatter', x='X', y='Y', color='green', label='Iris-setosa', ax=ax)
pos.ix[pos['Name']=='Iris-versicolor'].plot(kind='scatter', x='X', y='Y', color='red', label='Iris-versicolor', ax=ax)

需要注意,通过PCA降维实际上是损失了一些信息,我们也可以看一下保留的两个主成分可以解释原始数据的多少。
pca.fit(data.ix[:,:-1].values).explained_variance_ratio_
array([ 0.92461621, 0.05301557])
可以看到保留的两个主成分,第一个主成分可以解释原始变异的92.3%,第二个主成分可以解释原始变异的5.3%。也就是说降成两维后仍保留了原始信息的97.8%。
独立成分分析(ICA)
独立成分分析将多源信号拆分成最大可能独立性的子成分,它最初不是用来降维,而是用于拆分重叠的信号。
from sklearn import decomposition
pca = decomposition.FastICA(n_components=2)
X = pca.fit_transform(data.ix[:,:-1].values)
pos=pd.DataFrame()
pos['X'] =X[:, 0]
pos['Y'] =X[:, 1]
pos['Name'] = data['Name']
ax = pos.ix[pos['Name']=='Iris-virginica'].plot(kind='scatter', x='X', y='Y', color='blue', label='Iris-virginica')
ax = pos.ix[pos['Name']=='Iris-setosa'].plot(kind='scatter', x='X', y='Y', color='green', label='Iris-setosa', ax=ax)
pos.ix[pos['Name']=='Iris-versicolor'].plot(kind='scatter', x='X', y='Y', color='red', label='Iris-versicolor', ax=ax)

多维度量尺(Multi-dimensional scaling, MDS)
多维量表试图寻找原始高维空间数据的距离的良好低维表征。简单来说,多维度量尺被用于数据的相似性,它试图用几何空间中的距离来建模数据的相似性,直白来说就是用二维空间中的距离来表示高维空间的关系。数据可以是物体之间的相似度、分子之间的交互频率或国家间交易指数。这一点与前面的方法不同,前面的方法的输入都是原始数据,而在多维度量尺的例子中,输入是基于欧式距离的距离矩阵。多维度量尺算法是一个不断迭代的过程,因此,需要使用max_iter来指定最大迭代次数,同时计算的耗时也是上面算法中最大的一个。
from sklearn import manifold
from sklearn.metrics import euclidean_distances
similarities = euclidean_distances(data.ix[:,:-1].values)
mds = manifold.MDS(n_components=2, max_iter=3000, eps=1e-9, dissimilarity="precomputed", n_jobs=1)
X = mds.fit(similarities).embedding_
pos=pd.DataFrame(X, columns=['X', 'Y'])
pos['Name'] = data['Name']
ax = pos.ix[pos['Name']=='Iris-virginica'].plot(kind='scatter', x='X', y='Y', color='blue', label='Iris-virginica')
ax = pos.ix[pos['Name']=='Iris-setosa'].plot(kind='scatter', x='X', y='Y', color='green', label='Iris-setosa', ax=ax)
pos.ix[pos['Name']=='Iris-versicolor'].plot(kind='scatter', x='X', y='Y', color='red', label='Iris-versicolor', ax=ax)

看到以上几种算法的结果是不是觉得很神奇,相同类别的数据确实距离更近,尤其是后面几个降维算法的结果,基本上可以通过一些旋转或者坐标转换得到相似的图像。